一线三垂直问题解析:知识点、典型例题全掌握
<股票配资公司>一线三垂直问题解析:知识点、典型例题全掌握
【题型解析】
一线三垂直问题,通常指问题中有一线段绕某一点旋转 90°,或者问题中有矩形或正方形的情况下考虑,作辅助线构造全等三角形形或相似三角形,建立数量关系使问题得到解决。
【知识点总结】
① 过等腰直角三角形的直角顶点或者正方形直角顶点的一条直线。
② 过等腰直角三角形的另外两个顶点作该直线的垂线段一线三垂直问题解析:知识点、典型例题全掌握,会有两个三角形全等(AAS)。
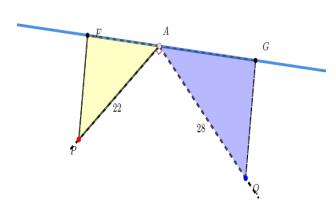
常见的两种图形:
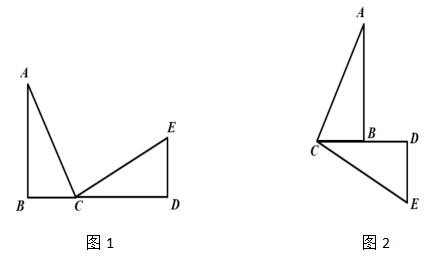
【典型例题】
1、已知:在等腰直角 ABC 中,∠BAC = 90°,AB = AC , E 是 AC 边上的 点,AF⊥BE 交 BC 于点 D, 若 AE = CD,
求证:① BF 平分 ∠ABC;② AB + AE = BC .
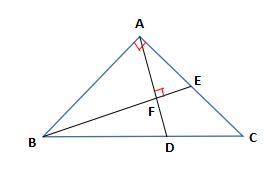
【解析】
(1)作 AC 的垂线交 AD 的延长线于点 M,
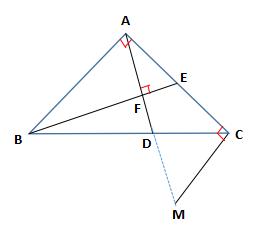
在 BAE 和 ACM 中,
∠ABE = ∠CAM = 90° - ∠BAF,AB = AC,∠BAE = ∠ACM = 90°,
∴ BAE≌ACM(ASA),
∴ CM = AE = CD等腰三角形三线合一证明,
∴ ∠M = ∠CDM = ∠AEB = ∠BAD,
∴ AB = BD,
又 ∵ BF⊥AD,
∴ BF 平分 ∠ABD(等腰三角形三线合一);
(2)AB + AE = BD + DC = BC .
2、已知:在 ABC 中,∠BAC = 90°,AB = AC,AE 是过点 A 的一条直线,且 BD⊥AE 于 D,CE⊥AE 于点 E.
① 当直线 AE 处于如图 1 的位置时,有 BD = DE + CE , 请说明理由;
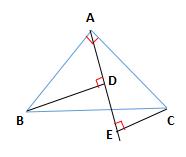
图 1
② 当直线 AE 处于如图 2 的位置时,则 BD、DE、CE 的关系如何?请说明理由.
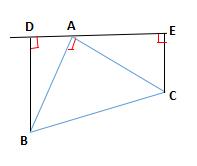
图 2
【解析】
(1)∵ BD⊥AE , CE⊥AE,
∴ ∠BDA = ∠AEC = 90°,
∴ ∠ABD + ∠BAD = 90°,
∵ ∠BAC = 90°,
∴ ∠BAD + ∠EAC = 90°,
∴ ∠ABD = ∠EAC,
在 ABD 和 CAE 中,

∠ADB = ∠CEA = 90° ,∠ABD = ∠EAC,AB=CA,
∴ ABD ≌ CAE (AAS),
AD = CE , BD = AE,
∵ AE = AD + DE,
∴ BD = DE + CE;
(2)在 ABD 和 CAE 中,
∠ADB = ∠CEA = 90° ,AB = CA,
∴ ABD ≌ CAE(AAS),
∴ AD=CE,BD=AE,
∵ AE = DE - AD,
∴ BD = DE - CE .
3、如图,在直角梯形 ABCD 中,AD∥BC,AB⊥BC , AD=2,BC=3,设 ∠BCD = α,以 D 为旋转中心,将腰 DC 绕点 D 逆时针旋转 90° 至 DE.
① 当 α=45° 时,求 EAD 的面积;
② 当 α = 30° 时,求 EAD 的面积;
③ 当 0°<α<90°,猜想 EAD 的面积与 α 大小有无关系,若有关,写出 EAD 的面积 S 与 α 的关系式,若无关,请证明结论.
【解析】
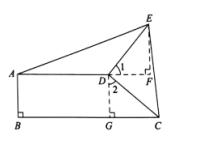
∵ AD∥BC , DG⊥BC,
∴ ∠GDF = 90°,
又 ∵ ∠EDC = 90°,
∴ ∠1 = ∠2,
在 CGD 和 EFD 中,
∠DGC = ∠DFE,∠1=∠2,CD = DE,
∴ DCG ≌ DEF,
∴ EF = CG,
∵ AD∥BC , AB⊥BC, AD = 2,BC = 3,
∴ BG = AD = 2,
∴ CG = 1,EF = 1,EAD 的面积与 α 无关 .