RTABC中与圆相关填空压轴题，求FG的长及解题分析？

<股票配资公司>RTABC中与圆相关填空压轴题，求FG的长及解题分析？

一、题目

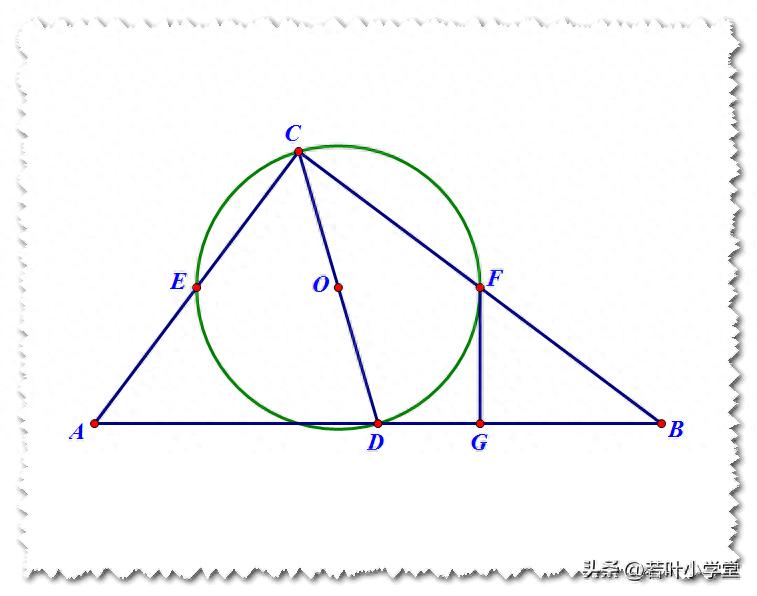
如图，在RTABC中，∠ACB=90°，AC=6，BC=8，点D是AB的中点，以CD为直径作圆O，圆O分别与AC、BC交于点E、F，过点F作圆O的切线FG，交AB于点G，则FG的长为.

二、分析与解答

这是一道与圆有关的填空压轴题，从考查频率上来讲，三角形出现的最多，然后是四边形，圆出现频率最低，而且难度也通常是最低的.

本题的得数很容易猜出来，O、D是中点等腰三角形三线合一证明，不难猜出F也是中点，且FG⊥AB

由BFG∽BAC或sin∠FBG=3/5，可得 FG=12/5.

本题的关键点就在于如何证明点F是中点.

解法一：由平行线分线段成比例来证点F是中点

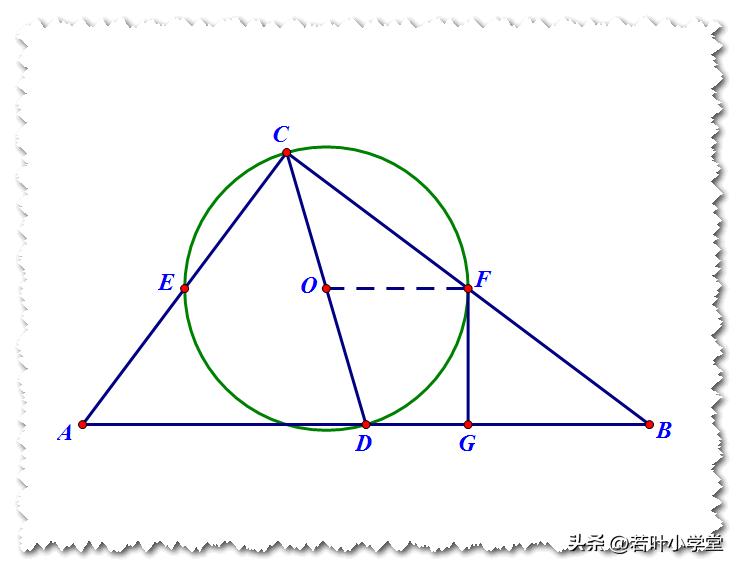
连接OF

∵FG为圆O的切线 ∴∠OFG=90°

∴∠OFC+∠BFG=90°

∵OC=OF ∴∠OFC=∠OCF

∵CD是RTABC斜边上的中线

∴CD=BD ∴∠OCF=∠B

∴∠OFC=∠B ∴OF//DB

∴∠BGF=∠OFG=90°，CF/BF=CO/OD=1（平行线分线段成比例）

∴BF=CF=4

由勾股定理可得 AB=√(6^2+8^2)=10

∴sin∠FBG=3/5

∴FG=4sin∠FBG=12/5

解法二：由等腰三角形的三线合一来证点F是中点

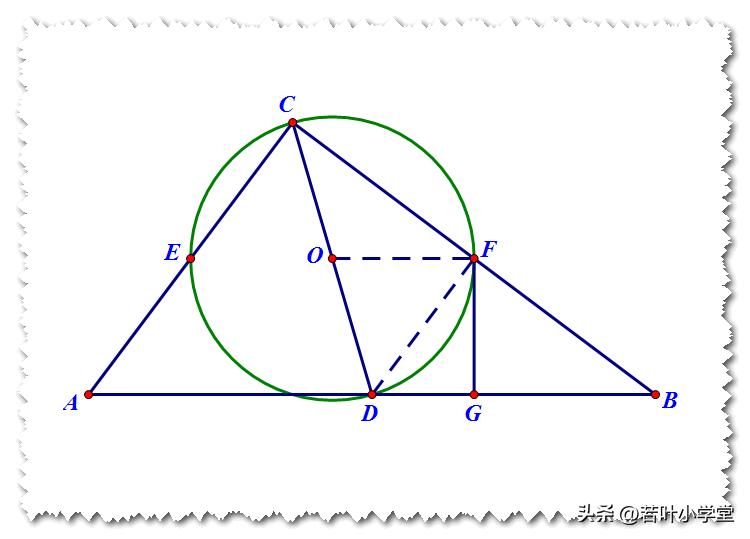
连接OF、DF

由等腰三角形的三线合一，可得F为中点

由中位线定理可得OF//DB，进而FG⊥DB

然后利用相似、三角函数或等面积法均可得到FG=12/5

也可以作ABC中AB边上的高，由等面积法得出高为24/5，然后由中位线定理得出FG=12/5

三、小结

1、关于圆的内容，课本上删减了很多，而且考的内容也很少，常见的有圆周角定理及其推论、切线的性质和判定、扇形的弧长和面积.

2、如果遇到切线，一定要记住连半径，遇切线、连半径、得垂直.本题中连半径就是一个必备的辅助线.

3、留两个小问题：

①点E是否是AC中点？

②设AD与圆O交于点HRTABC中与圆相关填空压轴题，求FG的长及解题分析？，CH与AB有什么样的位置关系？