例说等腰三角形的三线合一，你知道该如何灵活运用吗？

<股票配资公司>例说等腰三角形的三线合一，你知道该如何灵活运用吗？

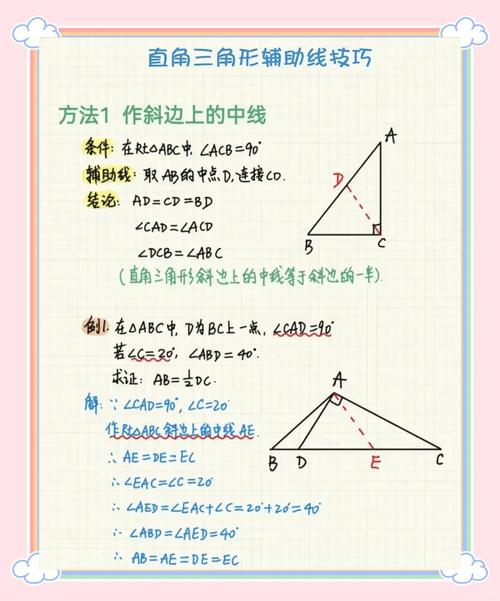
文档介绍：例说等腰三角形的“三线合一”济宁市梁山县小路口镇初级中学李丽(适用于人教版初二版10月刊)“三线合一”性质是等腰三角形所特有的重要性质,即等腰三角形底边上的中线、顶角的平分线、:如图1,ABC中,AB=AC,(1)若AD是等腰ABC底边BC上的中线,那么AD是顶角∠BAC的平分线,AD是底边BC上的高线;(2)若AD是等腰ABC顶角∠BAC的平分线,那么AD是底边BC上的中线,AD是底边BC上的高线;(3)若AD是等腰ABC底边BC上的高线,那么AD是顶角∠BAC的平分线,,“三线合一”性质给我们提供了证明角相等、直线垂直、,要注意灵活运用它们。下面仅举几例和同学们共同见识一下“三线合一”、证明角相等或倍数关系例1、已知:如图2等腰三角形的三线合一,在中,,:.【分析】作出等腰的顶角平分线将顶角分为相等的两部分,根据“三线合一”的性质证得等于其中任一部分即可.【证明】作的平分线AE,则有.∵,,∴(三线合一).∴.又∵,∴.∴.∴.【点拨】添加辅助线,利用等腰三角形的“三线合一”性质,巧妙地构造了两个具有同一锐角的直角三角形,将已知条件与待证结论有机地联系在一起,、如图3,在ABC中,AB=AC,BD=CD,DE⊥AB于E,DF⊥AC于F,求证:DE=【分析】:依题意,DE和DF分别为点D到∠BAC两边的距离,要证明它们相等,可先证明点D在∠BAC的平分线上,这只要证明AD是∠BAC的平分线.【证明】:连接AD.∵AB=AC,BD=CD,∴AD是等腰ABC底边BC上的中线.∴AD平分∠BAC.∵DE⊥AB于E,DF⊥AC于F,∴DE=DF.【点拨】能利用“三线合一”证明线段相等的问题,也可以用全等三角形来解决,但利用“三线合一”,我们在解决这类问题时,要纠正总是依据三角形全等的思维定势,应该优先选用“三线合一”、如图4,在ABC中,AB=AC,D在BA的延长线上,E在AC上,且AD=AE,求证:DE⊥【分析】:注意到ABC是以BC为底边的等腰三角形,⊥BC,应先证明DE与这条高平行.【证明】:过A作AF⊥BC于F.∵AB=AC,AF⊥BC于F,∴AF是等腰三角形ABC底边BC上的高线.∴AF平分∠BAC.∴∠BAC=2∠BAF.∵AD=AE,∴∠D=∠AED.∴∠BAC=∠D+∠AED=2∠D.∴∠BAF=∠D,DE∥AF.∴DE⊥BC.【点拨】当题设中同